Answer:
You can arrange the books 3,628,800 different ways.
Explanation:
You can imagine that the shelf has 10 "slots" where you can place a book. Each slot can take 1 of the 10 books. However, after you have placed 1 book, there are only 9 possible books to place. After 2 have been placed, there are only 8 possible.
Going left-to-right, the first slot has 10 available books.
Total combinations: 10
The 2nd slot has 9 available books.
Total combinations: 10 * 9
The 3rd slot has 8 available books.
Total combinations: 10 * 9 * 8
This continues for all 10 slots.
Eventually, for slot 10, there is only 1 book possible.
Total combinations: 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1
Multiply all numbers between 10 and 1 with each other is also known as "10 factorial" or "10!"
Thus, the total number of combinations is:
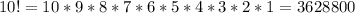
Answer: You can arrange the books 3,628,800 different ways.