Answer:
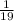
Explanation:
Let's let B represent the amount of blue cubes, Y represent the amount of yellow cubes, and G represent the amount of green cubes.
We know that there are three times as many blue cubes as yellow cubes. In other words:
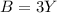
We also know that the are as five times as many green cubes as blue cubes. So:
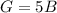
If Sarah takes a random cube, the chance it will be a yellow cube will be the total amount of yellow cubes over the total amount of cubes. In other words:
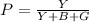
We can simplify this. Let's substitute 5B for G. This yields:
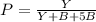
Combine like terms:
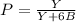
We can then substitute 3Y for B. This gives us:
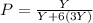
Multiply:

Again, add:
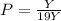
We can now cancel out the Y:

So, the chance of Sarah picking out a yellow cube is 1/19 or about 5.3% chance.
And we're done!