Question

MATH/MECHANICS (please helpp!!!)

A particle P starts from a fixed point O at time t =0, where t is in seconds and moves with constant acceleration in a straight line. The initial velocity of P is 1.5ms−1 and its velocity when t =10 is3.5ms−1.
(i)Find the displacement of P from O when t =10. [2]
Another particle Q also starts from O when t =0 and moves along the same straight line as P. The acceleration of Q at time t is 0.03t ms−2.
(ii)Given that Q has the same velocity as P when t = 10, show that it also has the same displacement from O as P when t =10.

Answer 1

• OP = 25 m
• OQ = 25 m

Explanation:

(i) Since acceleration is constant, velocity is a linear function of time. The average velocity over the interval will serve for the purpose of computing the displacement.

d = (v1+v2)/2×t = (1.5 m/s +3.5 m/s)/2·(10 s) = 25 m

P is displaced 25 meters from O when t=10.

__

(ii) Letting the initial velocity be represented by v1, we find the velocity as a function of time to be ...

`\displaystyle v(t)=v_1+\int_0^(t){a(t)}\,dt=v_1+\int_0^(t)0.03t\,dt=v_1+(0.03t^2)/(2)\\\\v(10)=v_1+0.015\cdot 10^2 = v_1+1.5\\\\3.5=v_1+1.5\ \rightarrow\ v_1=2.0\quad\text{m/s}\\\\v(t)=2.0+0.015t^2`

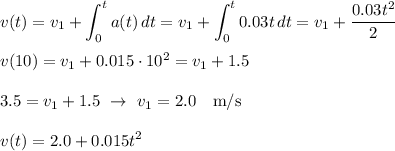
Then the displacement is the integral of velocity ...

`\displaystyle d=\int_0^(10){v(t)}\,dt=\int_0^(10){(2.0+0.015t^2)}\,dt\\\\d=2.0(10)+0.015\left((10^3)/(3)\right)=20+5=25`

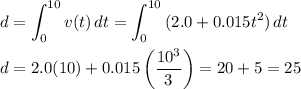
Q is also displaced 25 meters from O when t=10.