Question

Please help me!
Find the number x such that f(x) =1

Answer 1

D

Explanation:

We have the piecewise function:

`f(x) = \left\{ \begin{array}{ll} -(1)/(2)x-1 & \quad x \leq -2 \\ x & \quad x > -2 \end{array} \right.`

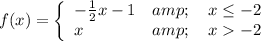
And we want to find x such that f(x)=1.

So, let's substitute 1 for f(x):

`1 = \left\{ \begin{array}{ll} -(1)/(2)x-1 & \quad x \leq -2 \\ x & \quad x > -2 \end{array} \right.`

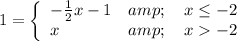
This has two equations. So, we can separate them into two separate cases. Namely:

`1=-(1)/(2)x-1\text{ or } 1=x`

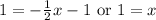
Let's solve for x in each case.

Case I:

We have:

`1=-(1)/(2)x-1`

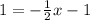
Add 1 to both sides:

`2=-(1)/(2)x`

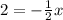
Let's cancel out the fraction by multiplying both sides by -2. So:

`2(-2)=(-2)(-1)/(2)x`

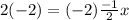
The right side cancels:

`-4=x\\`

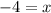
Flip:

`x=-4`

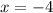
So, x is -4.

Case II:

We have:

`1=x`

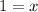
Flip:

`x=1`

This is the solution for our second case.

So, we have:

`x_1=-4\text{ or } x_2=1`

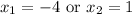
Now, can check to see if we have to to remove solution(s) that don't work.

Note that x=-4 is the solution to our first equation.

The first equation is defined only if x is less than -2.

-4 is less than -2. So, x=-4 is indeed a solution.

x=1 is the solution to our second equation.

The second equation is defined only if x is greater than or equal to -2.

1 is greater than or equal to -2. So, x=1 is also a solution.

Therefore, our two solutions are:

`x_1=-4\text{ or } x_2=1`

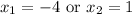
Out of our answer choices, we can pick D.

And we're done!