Answer:
See below.
Explanation:
To find the distance between any two points, we can use the distance formula:
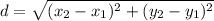
We want to prove that the distance between a point P(x,y) and the origin is:
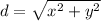
Remember that the origin is at (0,0).
So, let's prove it using the distance formula. Let's let the origin point (0,0) be (x₁, y₁) and let's let P(x, y) be (x₂, y₂). Substitute these values into the distance formula. This yields:
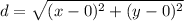
Subtract:
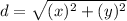
Simplify:
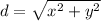
This is the same equation as given.
Q.E.D.