Question

#5 Air undergoes an adiabatic compression in a piston-cylinder assembly from P1= 1 atm and Ti=70 oF to P2= 5 atm. Employing ideal gas model with constant specific heat capacity ratio (Y), determine the work and heat transfer per unit mass if y = 1.5. (15 points)​

Answer 1

The work transfer per unit mass is approximately 149.89 kJ

The heat transfer for an adiabatic process = 0

Step-by-step explanation:

The given information are;

P₁ = 1 atm

T₁ = 70°F = 294.2611 F

P₂ = 5 atm

γ = 1.5

Therefore, we have for adiabatic system under compression

`T_(2) = T_(1)\cdot \left ((P_(2))/(P_(1)) \right )^{(\gamma -1)/(\gamma )}`

Therefore, we have;

`T_(2) = 294.2611 * \left ((5)/(1) \right )^{(1.5 -1)/(1.5 )} \approx 503.179 \ K`

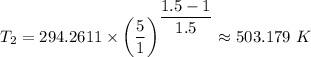
The p·dV work is given as follows;

`p \cdot dV = m \cdot c_v \cdot (T_2 - T_1)`

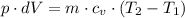
Therefore, we have;

Taking air as a diatomic gas, we have;

`C_v = (5* R)/(2) = (5* 8.314)/(2) = 20.785 \ J/(mol \cdot K)`

The molar mass of air = 28.97 g/mol

Therefore, we have

`c_v = (C_v)/(Molar \ mass) = (20.785)/(28.97) \approx 0.7175 \ kJ/(kg \cdot K)`

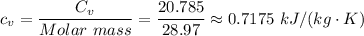
The work done per unit mass of gas is therefore;

`p \cdot dV =W = 1 * 0.7175 * (503.179 - 294.2611) \approx 149.89 \ kJ`

The work transfer per unit mass ≈ 149.89 kJ

The heat transfer for an adiabatic process = 0.