Answer:
a) The formula for the figure A is
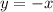 , b) The formula for the figure B is
, b) The formula for the figure B is
 -
-
Explanation:
From Analytical Geometry, we know that two lines are parallel to each other when they share the same slope. We get the slope of figure B by means of the slope formula:
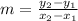
Where:
 ,
,
 - Initial and final x-coordinates, dimensionless.
- Initial and final x-coordinates, dimensionless.
 ,
,
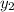 - Initial and final y-coordinates, dimensionless.
- Initial and final y-coordinates, dimensionless.
 - Slope, dimensionless.
- Slope, dimensionless.
If we know that
 and
and
 , the slope of both lines is:
, the slope of both lines is:

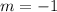
Any line is described by the following formula:
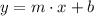
Where:
 - Independent variable, dimensionless.
- Independent variable, dimensionless.
 - Dependent variable, dimensionless.
- Dependent variable, dimensionless.
 - Slope, dimensionless.
- Slope, dimensionless.
 - y-Intercept, dimensionless.
- y-Intercept, dimensionless.
The y-Intercept is cleared within the formula:

Now we get the formula for each line depicted on figure:
a) The origin in figure a:
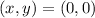 ,
,
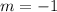

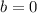
The formula for the figure A is
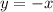 .
.
b) Point (0, 3) in figure b:
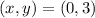 ,
,
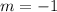
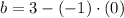

The formula for the figure B is
 -
-