Answer:
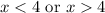
Explanation:
Solve we have the inequality:

Let's solve it like a normal equation first. So, pretend the inequality is an equal sign:

Solve for x. Zero Product Property:
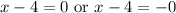
Add 4 to both sides for both equations:
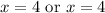
So, our roots are at x=4 and x=4.
Since our original inequality is greater than, this means that our solution will be all values to the left of our first zero and all values to the right of our second zero.
Therefore, our solution is:
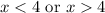
Simply put, our x can be anything except for 4 itself.
And we're done!