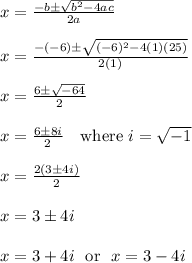Question

Solve the equation x^(2)-x=5x-25 over the complex numbers. Simplify the answer. Show your work.

soooo I'm asking this again in hopes that someone will help. I really don't know how to do this and if someone could help I would really appreciate it.

Answer 1

Answer: x = 3 + 4i and x = 3 - 4i

where i = sqrt(-1)

========================================================

Work Shown:

First get everything to one side

x^2-x = 5x-25

x^2-x-5x+25 = 0

x^2-6x+25 = 0

Now use the quadratic formula. We'll plug in a = 1, b = -6, c = 25

`x = (-b\pm√(b^2-4ac))/(2a)\\\\x = (-(-6)\pm√((-6)^2-4(1)(25)))/(2(1))\\\\x = (6\pm√(-64))/(2)\\\\x = (6\pm8i)/(2) \ \ \text{ where } i = √(-1)\\\\x = (2(3\pm4i))/(2)\\\\x = 3\pm4i\\\\x = 3+4i \ \text{ or } \ x = 3-4i\\\\`