Question

a ladder 10cm rest on a vertical wall of 8cm what is the distance of the vertical Wall from the Foot of the ladder ​

Answer 1

6 cm.

Explanation:

When you imagine the sentence, it is a right angled triangle. In this case, it's a Pythagoras Theorem. The formula for it is:

a²(opposite) + b²(adjacent) = c²(hypotenuse)

The vertical wall is the opposite, the distance between the foot of the ladder and the wall is the adjacent, while the ladder is the hypotenuse.

We have the measurements except for the adjacent. So it will be:

c² - a² = b²

10² - 8² = b²

100 - 64 = b²

36 = b²

√36 = b

b = 6 cm

The answer is 6 cm.

Answer 2

Hi there!

`\huge\boxed{6cm}`

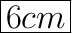
We can use the Pythagorean Theorem to solve:

Use the formula a² + b² = c² where:

"a" and "b" are the legs

"c" = Hypotenuse

The diagonal side, or the length of the ladder is 10cm, and one of the legs of the triangle is 8cm, therefore:

(8)² + b² = 10²

64 + b² = 100

Subtract 64 from both sides:

b² = 36

Take the square root of both sides:

√b² = √36

b = 6 cm. This is the distance of the wall from the foot of the letter.

Edit: Typo.