Question

Can someone thoroughly explain this implicit differentiation with a trig function. No matter how many times I try to solve this, I get it wrong. I’ve tried the quotient rule, and I’ve tried multiplying that (8 + x^2) to the other side to do the chain + product rule. I wanna know where I went wrong

Answer 1

`(dy)/(dx)=y'=(\sec^2(x-y)(8+x^2)^2+2xy)/((8+x^2)(1+\sec^2(x-y)(8+x^2)))`

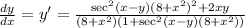
Explanation:

So we have the equation:

`\tan(x-y)=(y)/(8+x^2)`

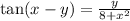
And we want to find dy/dx.

So, let's take the derivative of both sides:

`(d)/(dx)[\tan(x-y)]=(d)/(dx)[(y)/(8+x^2)]`

Let's do each side individually.

Left Side:

We have:

`(d)/(dx)[\tan(x-y)]`

We can use the chain rule, where:

`(u(v(x))'=u'(v(x))\cdot v'(x)`

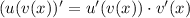
Let u(x) be tan(x). Then v(x) is (x-y). Remember that d/dx(tan(x)) is sec²(x). So:

`=\sec^2(x-y)\cdot ((d)/(dx)[x-y])`

Differentiate x like normally. Implicitly differentiate for y. This yields:

`=\sec^2(x-y)(1-y')`

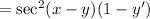
Distribute:

`=\sec^2(x-y)-y'\sec^2(x-y)`

And that is our left side.

Right Side:

We have:

`(d)/(dx)[(y)/(8+x^2)]`

We can use the quotient rule, where:

`(d)/(dx)[f/g]=(f'g-fg')/(g^2)`

f is y. g is (8+x²). So:

`=((d)/(dx)[y](8+x^2)-(y)(d)/(dx)(8+x^2))/((8+x^2)^2)`

Differentiate:

`=(y'(8+x^2)-2xy)/((8+x^2)^2)`

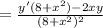
And that is our right side.

So, our entire equation is:

`\sec^2(x-y)-y'\sec^2(x-y)=(y'(8+x^2)-2xy)/((8+x^2)^2)`

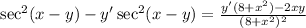
To find dy/dx, we have to solve for y'. Let's multiply both sides by the denominator on the right. So:

`((8+x^2)^2)\sec^2(x-y)-y'\sec^2(x-y)=(y'(8+x^2)-2xy)/((8+x^2)^2)((8+x^2)^2)`

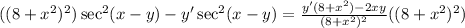
The right side cancels. Let's distribute the left:

`\sec^2(x-y)(8+x^2)^2-y'\sec^2(x-y)(8+x^2)^2=y'(8+x^2)-2xy`

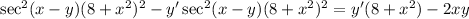
Now, let's move all the y'-terms to one side. Add our second term from our left equation to the right. So:

`\sec^2(x-y)(8+x^2)^2=y'(8+x^2)-2xy+y'\sec^2(x-y)(8+x^2)^2`

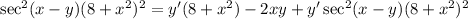
Move -2xy to the left. So:

`\sec^2(x-y)(8+x^2)^2+2xy=y'(8+x^2)+y'\sec^2(x-y)(8+x^2)^2`

Factor out a y' from the right:

`\sec^2(x-y)(8+x^2)^2+2xy=y'((8+x^2)+\sec^2(x-y)(8+x^2)^2)`

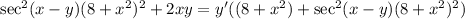
Divide. Therefore, dy/dx is:

`(dy)/(dx)=y'=(\sec^2(x-y)(8+x^2)^2+2xy)/((8+x^2)+\sec^2(x-y)(8+x^2)^2)`

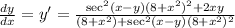
We can factor out a (8+x²) from the denominator. So:

`(dy)/(dx)=y'=(\sec^2(x-y)(8+x^2)^2+2xy)/((8+x^2)(1+\sec^2(x-y)(8+x^2)))`

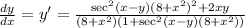
And we're done!