Answer:
![\huge\boxed{\sqrt[9]{3}}](https://img.qammunity.org/2021/formulas/mathematics/college/nbghdbgzryjja9l1zei13tsry284cewrfb.png)
Explanation:
In order to convert the expression
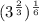 into a radical, we need to simplify it down first.
into a radical, we need to simplify it down first.
Using exponent rules, we know that
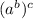 can be simplified to
can be simplified to
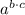 .
.
Therefore we can say that
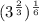 is the same as
is the same as
 .
.
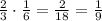
So we have
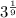 .
.
When we have a number to a fraction power, it's the same thing as taking the denominator root of the base to the numerator power.
Basically:
If we have
 :
:
We'll take the denominator root (the denominator is 4) of the base (2):
![\sqrt[4]{2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/ddu6i7qcjrgpxmeub8upmo0sr1mmrfhm.png)
But inside the radical, we raise the base to the numerator (3) power.
![\sqrt[4]{2^3}](https://img.qammunity.org/2021/formulas/mathematics/college/bthbqothavloa6gieresep4p6uvhm0yfgy.png)
Same logic for
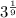
![\sqrt[9]{3^1}](https://img.qammunity.org/2021/formulas/mathematics/college/k4xjjs10pve66uiw3rtz5wiv0jynu3pstc.png)
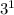 is the same as 3.
is the same as 3.
![\sqrt[9]{3}](https://img.qammunity.org/2021/formulas/mathematics/high-school/zcypf0agdagzl3ulxaeghnb2jly517llzs.png)
Hope this helped!