Answer:
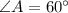
Explanation:
So we have the following parallelogram and we wish to solve for ∠A.
To do so, we will need to solve for x first. Look carefully at the parallelogram...
Notice that ∠A and ∠D are consecutive angles. In other words:
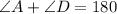
Since we have an equation for ∠D, substitute:
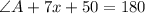
Notice that ∠A and ∠B are also consecutive angles. So:
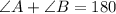
We know the equation for ∠B. Substitute:
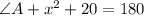
Since both equations equal 180, we can set them equal to each other:
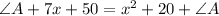
Let's subtract ∠A from both sides. This gives us:

Now, we can solve for x. This is a quadratic, so let's move all the terms to one side. To start off, let's subtract 50 from both sides:
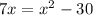
Now, let's subtract 7x from both sides:

Solve for x. We can factor.
Here's the trick to factoring. If we have the following:
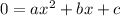
The we will need to find two numbers, p and q, such that:
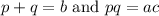
In our equation, a is 1, b is -7, and c is -30.
So, we want two numbers that sum to -7 and multiply to (1)(-30)=-30.
We can use -10 and 3. -10+3 is -7 and -10(3) is -30. So, let's substitute our b term for -10x and 3x. In other words, we have:

Substitute -7x for 3x-10x. This gives us:
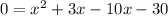
This is equivalent to our old equation.
Now, we can factor. Factor out a x from the first two terms:
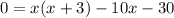
And factor out a -10 from the two last terms:
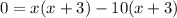
Since the expressions within the parentheses are the same, we can use grouping to acquire:
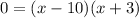
Note that this is essentially the distribute property. If we distribute, we will get the same as above.
Zero Product Property:
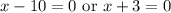
Solve for x:

So, we have two cases for x. Each case will yield a different answer for ∠A.
Case I: x=10
Use our original equation of:
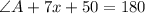
Substitue 10 for x:
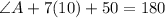
Multiply:

Add:

Subtract 120 from both sides:
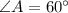
So, in our first case, ∠A is 60°
Case II: x=-3
Again, same equation:
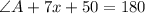
This time, substitute -3 for x. This yields:
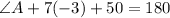
Multiply:

Add:
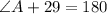
Subtract 29 from both sides:
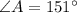
So, in our second case, ∠A is 151°
However, 151° doesn't seem likely with how the figure is drawn.
Therefore, our final answer is 60°.
And we're done!
Edit: Fixed Incorrect Answer