Question

The equations of three lines are given below.

Line 1: -3y = 5x + 6
Line 2: 10x - 6y=-4
3
Line 3: y=-=x+3
5
For each pair of lines, determine whether they are parallel, perpendicular, or neither.
Line 1 and Line 2:
Parallel O Perpendicular ONeither
x
3
?
Line 1 and Line 3:
Parallel Perpendicular
Neither
Line 2 and Line 3: Parallel Perpendicular Neither
I Don't Know
Submit
Submit
2020 M

Answer 1

Explanation:

Hey there!

Here, The equations are;

-3y=5x+6

5x+3y+6=0.........(i)

10x-6y+4 =0......(ii)

y= -3/5x+3.......(iii)

From equation (i).

`slope(m1) = ( - coeff. \: ofx)/(coeff. \: of \: y)`

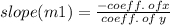
Put all values.

`m1 = ( - 5)/(3)`

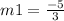
Now, from equation (ii).

`m2 = ( - coeff. \: of \: x)/(coeff. \: of \: y)`

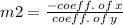
Put all values.

`m2 = ( - 10 )/( - 6)`

`m2 = (5)/(3)`

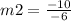
As m1 is not equal to m2 it is not parallel lines.

For perpendicular lines;

m1×m2= -1.

`( - 5)/(3) * (5)/(3)`

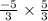
After simplifying it we get -25/9 which is not equal to-1. So, it is not perpendicular lines.

Therefore, the lines are neither parallel nor perpendicular.

But the lines of equation (ii) and (iii) are perpendicular to eachother.

-3/5×5/3= -1

[ so, the line (ii) and (iii) are perpendicular to eachother but others are neither]

Hope it helps...

Answer 2

line 1&2 are neither

line 1&3 are also neither

lines 2 and 3 however are perpendicular since they make 90 degree angles when they meet.

Explanation: