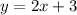Answer:
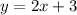
Explanation:
The slope-intercept form is
 , where
, where
 is the slope and
is the slope and
 is the y-intercept.
is the y-intercept.

Using the slope-intercept form, the slope is 2.
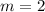
So in order for us to find an equation that is parallel, the slopes must be equal. We need to find the parallel line using the point-slope formula.
We use the slope 2 and a given point
 to substitute for x1 and y1 in the point-slope form
to substitute for x1 and y1 in the point-slope form
 , which is derived from the slope equation:
, which is derived from the slope equation:

Now we simplify the equation and keep it in point-slope form.
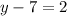 ×
×

Simplify
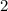 ×
×

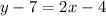
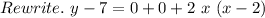

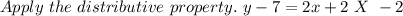
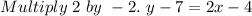
Last, We move all terms not containing y to the right side of the equation.
Add 7 to both sides of the equation.
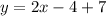
Add −4 and 7 and your answer will be: