Question

In which line did the student make the first mistake?

Answer 1

It’s line 4. She subtracted the final from the initial. The distance formula requires you to subtract the initial from the final. That’s the formula for displacement in x and y.

Answer 2

The student's initial assertion in line 1, stating that AB = 2 and FD = 2, lacks justification for congruence. The corrected proof introduces proper justifications and calculations, rectifying the initial mistake. Option a is the correct choice.

In line 1, the student states that AB = 2 and FD = 2. However, this is not necessarily true, because the student has not shown that the two segments are congruent.

To show that two segments are congruent, we need to show that they have the same length and angle measures. The student has only shown that AB and FD have the same length. Therefore, the student cannot conclude that AB is congruent to FD in line 1.

The student's mistake in line 1 propagates to the rest of the proof. In line 2, the student states that \overline{AB}\cong\overline{FD}. However, this is not true, because the student has not shown that AB is congruent to FD.

Therefore, the student made the first mistake in line 1.

Here is a corrected version of the proof:

Line 1: \[AB=2\]

Line 2: \[|FD=2\]

Line 3:
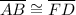`\overline{AB}\cong\overline{FD}` (This line is incorrect. The student has not shown that AB is congruent to FD.)

Line 4: ZA F

Line 5: Length of AC.

A (1, 2)

\[C(3,3)\]

`\[d=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}\]`

`\[d=\sqrt{(3-1)^(2)+(3-2)^(2)}\]`

`\[d=\sqrt{(2)^(2)+(1)^(2)}\]`

`\[d=√(4+1)\]`

`\[d=√(5)\]`

`\[\overline{AC}=2.23\]`

Line 6: Length of EF.

`\[F(3,2)\\ F(5,3)\end{cases}\]`

`\[d=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}\]`

DA

63°

The student can then proceed to calculate the length of EF in line 6. Once the length of EF is known, the student can show that triangle ABC is congruent to triangle EFD by HL (hypotenuse-leg).

Therefore, the student made the first mistake in line 1. So, Option a is the correct choice.