Question

What is g^-1(x)? What is the domain of g^-1(x)?

Please help!! It’ll be greatly appreciated!!

Answer 1

Answer:
`g^(-1)(x) = (1-4x)/(x)`

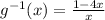
Domain of the inverse is any real number but x cannot equal zero

Domain in set builder notation =
`\{x | x\in\mathbb{R} , \ x \\e 0\}`

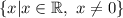
Domain in interval notation =
`(-\infty, 0) \cup (0, \infty)`

================================================

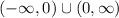
Let's make h(x) be the inverse of g(x)

g(x) = 1/(x+4) is the same as y = 1/(x+4).

To find the inverse, we swap x and y, then solve for y like so....

y = 1/(x+4)

x = 1/(y+4) .... x and y swap

x(y+4) = 1

xy+4x = 1

xy = 1-4x

y = (1-4x)/x

h(x) = (1-4x)/x is the inverse of g(x)

We can verify this by showing that g(h(x)) = x and h(g(x)) = x. I'll leave that for you to confirm.

The domain of h(x) is the set of real numbers x such that x cannot be 0. So x can be anything but 0. In set builder notation, we would say
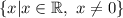`\{x | x\in\mathbb{R} , \ x \\e 0\}` and in interval notation that is
`(-\infty, 0) \cup (0, \infty)`

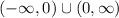
We kick out x = 0 so that (1-4x)/x doesn't have any division by zero errors.