Answer:
 has units of distance
has units of distance
 has units of distance over time
has units of distance over time
 has units of distance over
has units of distance over

 has units of distance over
has units of distance over
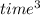
Step-by-step explanation:
Since the expression for the distance is:
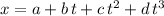
then:
 has units of distance
has units of distance
 has units of distance over time
has units of distance over time
 has units of distance over
has units of distance over

 has units of distance over
has units of distance over
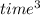
because we are supposed to be able to add all of the terms and get a distance. So the products on each term that contains factors of time (t) should be cancelling those time units with units in the denominator of the multiplicative constant s that accompany them.