Question

PLEASE HELPPP Today in Algebra class, Ethan learned about the expressions (1+ 1/x)^x and e, but he can't remember if (1+1/x)^x gets closer and closer to e as x gets larger and larger, or if (1+1/x)^x get further and further away from e as x gets larger and larger. He's going to do a test to figure it out.

part l:What is the value of e to five decimal places?
Part II: What is the value of (1+1/x)^x when x = 5? Give your answer to five decimal places.
Part III: What is the value of (1+1/x)^x when x = 25? Give your answer to five decimal places.
Part IV: What is the value of (1+1/x)^x when x = 125? Give your answer to five decimal
places.
Part V: Is (1+1/x)^x getting closer and closer to e as x is getting larger and larger, or is getting further and further away from e as x is getting larger and larger?

Answer 1

Part 1

Use your calculator to have it display
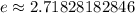`e \approx 2.71828182846` and round that to five decimal places to get
`e \approx 2.71828`

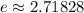
Answer: 2.71828

=============================================

Part 2

Plug in x = 5 to get

`y = \left(1 + (1)/(x)\right)^x\\\\y = \left(1 + (1)/(5)\right)^5\\\\y = 2.48832\\\\`

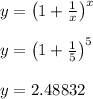
Answer: 2.48832

=============================================

Part 3

Now plug in x = 25

`y = \left(1 + (1)/(x)\right)^x\\\\y = \left(1 + (1)/(25)\right)^(25)\\\\y \approx 2.66583633148742\\\\y \approx 2.665 84\\\\`

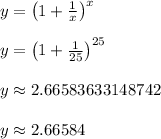
Answer: 2.66584

=============================================

Part 4

Plug in x = 125

`y = \left(1 + (1)/(x)\right)^x\\\\y = \left(1 + (1)/(125)\right)^(125)\\\\y \approx 2.70748783321031\\\\y \approx 2.70749\\\\`

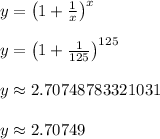
Answer: 2.70749

=============================================

Part 5

As x gets larger, it appears (1+1/x)^x is getting closer and closer to e = 2.71828 since the sequence of answers (from parts 2 through 4) was 2.48832, 2.66584, 2.70749.