Answer:
Explanation:
As first step we must obtain the equation of the line. According to Analytical Geometry, we can get a equation of the line by knowing two different points. A linear function is represented by the following expression:
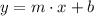
Where:
 - Independent variable, dimensionless.
- Independent variable, dimensionless.
 - Dependent variable, dimensionless.
- Dependent variable, dimensionless.
 - Slope, dimensionless.
- Slope, dimensionless.
 - y-Intercept, dimensionless.
- y-Intercept, dimensionless.
If we know that
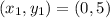 and
and
 , the following system of linear equations is formed:
, the following system of linear equations is formed:
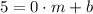
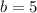 (Eq. 1)
(Eq. 1)
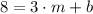
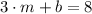 (Eq. 2)
(Eq. 2)
From (Eq. 1) in (Eq. 2) we get the value of
 :
:


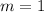
The equation of the line that contains the points (0, 5) and (3, 8) is
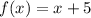 .
.
As next step we must apply a reflection in the x-axis, whose operation is defined as follows:

That is:
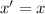
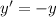
Then, the function
 is
is
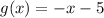 . We plot each function and include the result in the attachment below.
. We plot each function and include the result in the attachment below.