
Write an equation of the line passing through (6, -9) and has a slope of -3.

First, we need to write the equation in point-slope form:-
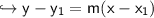
- Replace y₁ with -9, m with 3, and x₁ with 6:-
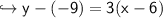
 On simplification,
On simplification,
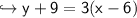
 On further simplification,
On further simplification,
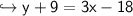
 Subtract 9 from both sides, which results in:-
Subtract 9 from both sides, which results in:-
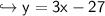
So we conclude that Option B is correct.
Good luck with your studies.
