Answer:
Length =
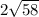
Step-by-step explanation:
The width of the triangle is 6 cm. We are given the area. Lets work through this step by step.
First of all, the area of a triangle is
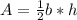
We know that the breadth, or the base, b, is 6 cm.
Substitute the value of 6 for B

What we need to do is find the length of the height, H. Therefore
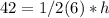
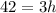
Divide each side by 3 to isolate h
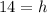
The height is 14.
In order to determine the length, just substitute the values of 6 and 14 for a^2 and b^2 in the pythagorean theorem.
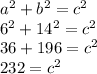
Take the square root of both sides to simplify c.
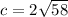
This is approximately equal to
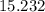 cm's
cm's