Question

Susan made a graph that represents the amount of money she spends on

lunch, y, for the number of days she is in school, x. The graph is a straight
line that passes through the origin and the point (1, 2.5).
Which statement(s) must be true? Select all that apply.
The slope of the graph is 2.5.
The y-intercept of the graph is 2.5.
Susan is in school for 2.5 days.
Susan spends $2.50 on lunch per day.

Answer 1

The slope of the graph is 2.5.

Susan spends $2.50 on lunch per day.

Explanation:

Given

`Point: (0,0)\ to\ (1,2.5)`

Required

Which of the given options is true

First, we need to determine the slope (m)

`m = (y_2 - y_1)/(x_2 - x_1)`

`m = (2.5 - 0)/(1 - 0)`

`m = (2.5)/(1)`

`m = 2.5`

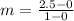
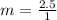
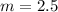
This implies that the first option is true

Next, we determine the line equation using:

`y - y_1 = m(x - x_1)`

This gives:

`y - 0 = 2.5(x - 0)`

`y = 2.5x`

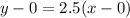
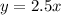
Substitute 0 for x to determine the y intercept

`y = 2.5* 0`

`y = 0`

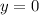
This implies that the second option is false

The third option is also false

Take x as 1

`y = 2.5 * 1`

Take x as 2

`y = 2.5 * 2 = 5.0`

Take x as 3

`y = 2.5 * 3 = 7.5`

The presence of 2.5 in the equations above indicates that Susan spends $2.50 on lunch daily.

Hence, the fourth option is correct