Answer:
Measure of one angle is required.
Explanation:
Kindly refer to the image attached.
AM and BN are the two parallel lines cut by a transversal PQ.
The angles formed are:
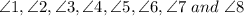 .
.
Let, only one of the angles is known to us.
Let, it is given that
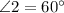
AM is a straight line, therefore
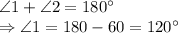
 and
and
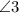 are vertically opposite angles, therefore must be equal to each other.
are vertically opposite angles, therefore must be equal to each other.
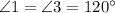
 and
and
 are vertically opposite angles, therefore must be equal to each other.
are vertically opposite angles, therefore must be equal to each other.
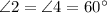
By Corresponding angle postulate, we can see the following:
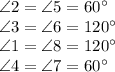
Therefore, by knowing just one angle, all the angles can be found.