Question

A company that produces footballs uses a proprietary mixture of ideal gases to inflate their footballs. If the temperature of 230 grams [g] of gas mixture in a 15-liter [L] tank is maintained at 465 degrees Rankine [°R] and the tank is pressurized to 135 pound-force per square inch [psi], what is the molecular weight of the gas mixture in units of grams per mole

Answer 1

The molecular weight of the gas mixture is 35.38 g/mol.

Step-by-step explanation:

The molecular weight of the gas can be found using the following equation:

`M = (m)/(n)`

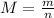
Where:

m: is the mass = 230 g

n: is the number of moles

First, we need to find the number of moles using Ideal Gas Law:

`PV = nRT`

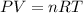
Where:

P: is the pressure = 135 psi

V: is the volume = 15 L

R: is the gas constant = 0.082 L*atm/(K*mol)

T: is the temperature = 465 °R (K = R*5/9)

`n = (PV)/(RT) = (135 psi*(1 atm)/(14.6959 psi)*15 L)/(0.082 L*atm/(K*mol)*465*(5/9) K) = 6.50 moles`

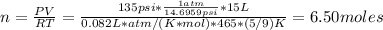
Finally, the molecular weight of the gas is:

`M = (m)/(n) = (230 g)/(6.50 moles) = 35.38 g/mol`

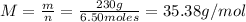
Therefore, the molecular weight of the gas mixture is 35.38 g/mol.

I hope it helps you!