Answer:
1 + i
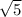 , 1 - i
, 1 - i
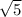
Explanation:
A quadratic function is f(x) = a
 + bx + c
+ bx + c
Your function with the given values is f(x) = 2
 - 4x + 12
- 4x + 12
To solve a quadratic function, you can use the quadratic formula
(-b +/-
 ) / 2a
) / 2a
Fill in with your given values.
(4 +/-
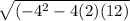 ) / 2(2)
) / 2(2)
Simplify
(4 +/-
 ) / 4
) / 4
(4 +/-
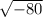 ) / 4
) / 4
Because there is a negative number under the square root making it an imaginary number put an i by it.
(4 +/- i
 ) / 4
) / 4
80 is divisible by 16, a perfect square. 80 / 16 = 5
(4 +/- 4i
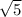 ) / 4
) / 4
Divide by 4
1 +/- i
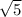
Your teacher may want you to list your radical without the i and just as
 , so keep that in mind.
, so keep that in mind.
Don't forget to list it both as addition and subtraction.