Question

What is the value of f^-1(0)?



Please help! It’ll be greatly appreciated!

Answer 1

`f^(-1)(0)=6`

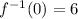
Explanation:

So, we have the graph y=f(x).

And we want to find:

`f^(-1)(0)`

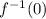
Remember that the inverse of a function is simply the x-values and y-values swapped. To see this, let's let our inverse equal y:

`f^(-1)(0)=y`

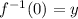
This means that we have the point:

`(0,y)`

So, to find our solution, we will swap the x- and y-coordinates. This gives us:

`(x,0)`

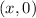
So, simply need to find the x-coordinate such that y is 0.

From our graph, we can see the point (6,0). In other words:

`f(6)=0`

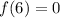
So:

`f^(-1)(0)=6`

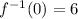
And we're done!