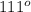Answer:
m<EFG =
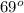 , and m<GFH =
, and m<GFH =
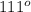
Explanation:
Linear pair angles are two supplementary angles.
Thus,
m<EFG + m<GFH =
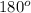
2n + 21 + 4n + 15 =
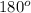
collecting like terms, we have:
6n + 36 =
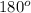
6n =
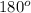 - 36
- 36
6n =
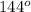
divide both both sides by 6,
n =
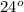
Therefore,
m<EFG = 2n + 21
= 2 x
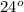 + 21
+ 21
= 48 + 21
=
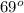
m<GFH = 4n + 15
= 4 x
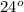 + 15
+ 15
= 96 + 15
=
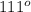
Thus m<EFG =
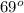 , and m<GFH =
, and m<GFH =