Let the rocket is launched at an angle of \theta with respect to the positive direction of the x-axis with an initial velocity u=15m/s.
Let the initial position of the rocked is at the origin of the cartesian coordinate system where the illustrative path of the rochet has been shown in the figure.
As per assumed sine convention, the physical quantities like displacement, velocity, acceleration, have been taken positively in the positive direction of the x and y-axis.
Let the point P(x,y) be the position of the rocket at any time instant t as shown.
Gravitational force is acting downward, so it will not change the horizontal component of the initial velocity, i.e.
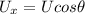 is constant.
is constant.
So, after time, t, the horizontal component of the position of the rocket is

The vertical component of the velocity will vary as per the equation of laws of motion,
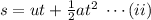 , where,s, u and a are the displacement, initial velocity, and acceleration of the object in the same direction.
, where,s, u and a are the displacement, initial velocity, and acceleration of the object in the same direction.
(a) At instant position P(x,y):
The vertical component of the initial velocity is,
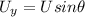 .
.
Vertical displacement =y
So, s=y
Acceleration due to gravity is
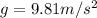 in the downward direction.
in the downward direction.
So,
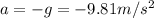 (as per sigh convention)
(as per sigh convention)
Now, from equation (ii),
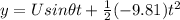
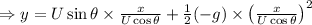
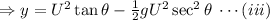
This is the required, quadratic equation, where
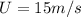 and
and
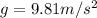 .
.
(b) At the highest point the vertical velocity,v, of the rocket becomes zero.
From the law of motion,

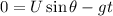
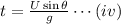
The rocket will reach the maximum height at
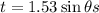
So, from equations (ii) and (iv), the maximum height,
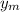 is
is
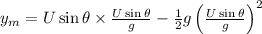
In the case of vertical launch,
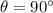 , and
, and
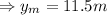 and
and
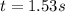 .
.
Height from the ground= 11.5+3=14.5 m.
(c) Height of rocket after t=4 s:

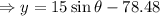
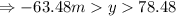
This is the mathematical position of the graph shown which is below ground but there is the ground at
 , so the rocket will be at the ground at t=4 s.
, so the rocket will be at the ground at t=4 s.
(d) The position of the ground is, y=-3m.


Solving this for a vertical launch.
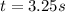 and
and
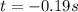 (neglecting the negative time)
(neglecting the negative time)
So, the time to reach the ground is 3.25 s.
(e) Height from the ground is 13m, so, y=13-3=10 m
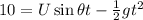
Assume vertical launch,
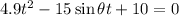 [using equation (ii)]
[using equation (ii)]
 and
and
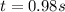
There are two times, one is when the rocket going upward and the other is when coming downward.