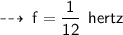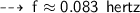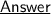
As we know, period (t)of a wave and it's frequency (f) are Reciprocal of each other, so if one is know then we can just reverse the order to get the other one.
that is :

Now, let's move on to problems ~
# 11. f = 15 hertz, t = ?
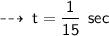
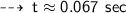
#12. f = 292 hertz, t = ?
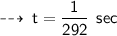
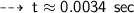
#13. t = 12 seconds, f = ?