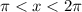Question

Over which interval is the graph of y= cos(x) strictly increasing?

A. 0 B. 0 C.pi/2D. Pi< x <2pi

Answer 1

D.
`\pi<x<2\pi`

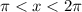
Explanation:

Given the function

`y=cosx`

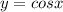
Kindly refer to the graph attached in the answer area.

Referring to the intervals [0,
`2\pi`].

It decreases from the interval [0,
`\pi`] and then starts increasing in the interval

`[\pi,2\pi]`.

Proving by taking derivative:

Taking derivative of the function,
`y=cosx`

`(dy)/(dx)=-sinx`

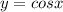
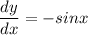
In the interval
`[\pi,2\pi]`,
`sinx` is negative i.e.
`sinx<0`.

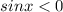Therefore
`-sinx>0`

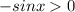
When, the derivative of a function is positive, then the function is strictly increasing.

So, the answer is:

D.
`\pi<x<2\pi`