Question

Use implicit differentiation to find the slope of the tangent line at the given point:

Answer 1

`\displaystyle (dy)/(dx)\Big|_((1, 1))=0`

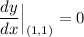
Explanation:

We are given the equation:

`(x^2+y^2)^2=4x^2y`

And we want to find the slope of the tangent line at the point (1,1).

Recall that the slope of the tangent line to a point of a function is given by the function's derivative.

Thus, find the derivative of the equation. Take the derivative of both sides with respect to x:

`\displaystyle (d)/(dx)\left[(x^2+y^2)^2\right]=(d)/(dx)\left[4x^2y\right]`

Let's do each side individually.

Left:

We can use the chain rule:

`(u(v(x))'=u'(v(x))\cdot v'(x)`

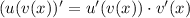
Let v(x) be x² + y² and u(x) is x². Thus, u'(x) is 2x. Therefore:

`\displaystyle (d)/(dx)\left[(x^2+y^2)^2\right]=2\left(x^2+y^2\right)\left((d)/(dx)\left[x^2+y^2\right]\right)`

Differentiate:

`\displaystyle (d)/(dx)[(x^2+y^2)^2]=2(x^2+y^2)\left(2x+2y(dy)/(dx)\right)`

Factor. Therefore, our left side is:

`\displaystyle 4(x^2+y^2)\left(x+y(dy)/(dx)\right)`

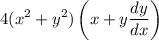
Right:

We have:

`\displaystyle (d)/(dx)\left[4x^2y\right]`

We can move the constant multiple outside:

`\displaystyle =4(d)/(dx)\left[x^2y\right]`

We will use the Product Rule:

`\displaystyle =4\left((d)/(dx)\left[x^2\right]y+x^2(d)/(dx)\left[y\right]\right)`

Differentiate:

`\displaystyle =4\left(2xy+x^2(dy)/(dx)\right)`

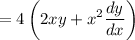
Therefore, our entire equation is:

`\displaystyle 4(x^2+y^2)\left(x+y(dy)/(dx)\right)=4\left(2xy+x^2(dy)/(dx)\right)`

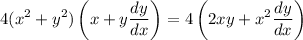
To find the derivative at (1,1), substitute and evaluate dy/dx when x = 1 and y = 1. Hence:

`\displaystyle 4((1)^2+(1)^2)\left((1)+(1)(dy)/(dx)\right)=4\left(2(1)(1)+(1)^2(dy)/(dx)\right)`

Evaluate:

`\displaystyle 4((1)+(1))\left(1+(dy)/(dx)\right)=4\left(2+(dy)/(dx)\right)`

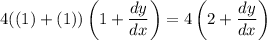
Further simplify:

`\displaystyle 8\left(1+(dy)/(dx)\right)=8+4(dy)/(dx)`

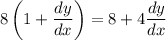
Distribute:

`\displaystyle 8+8(dy)/(dx)=8+4(dy)/(dx)`

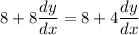
Solve for dy/dx:

`\displaystyle 4(dy)/(dx)=0\Rightarrow (dy)/(dx)=0`

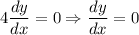
Therefore, the slope of the tangent line at the point (1, 1) is 0.