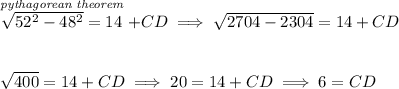Check the picture below, on the left side.
since the triangle ABC is an isosceles with twin sides, if we drop a line bisecting the angle at the vertex A, we end up with a perpendicular line that cuts the "base" in two equal halves, so then

as you can see in the picture in red, now let's find CD.