Answer:
a) h = 0.1:
 , h = 0.01:
, h = 0.01:
 , h = 0.001:
, h = 0.001:
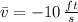 , b) The instantaneous velocity of the ball when
, b) The instantaneous velocity of the ball when
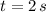 is
is
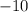 feet per second.
feet per second.
Explanation:
a) We know that
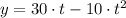 describes the position of the ball, measured in feet, in time, measured in seconds, and the average velocity (
describes the position of the ball, measured in feet, in time, measured in seconds, and the average velocity (
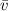 ), measured in feet per second, can be done by means of the following definition:
), measured in feet per second, can be done by means of the following definition:
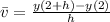
Where:
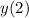 - Position of the ball evaluated at
- Position of the ball evaluated at
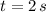 , measured in feet.
, measured in feet.
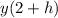 - Position of the ball evaluated at
- Position of the ball evaluated at
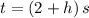 , measured in feet.
, measured in feet.
 - Change interval, measured in seconds.
- Change interval, measured in seconds.
Now, we obtained different average velocities by means of different change intervals:
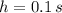
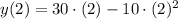
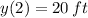

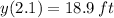
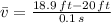

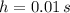
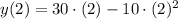
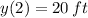
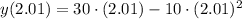
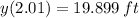
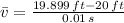

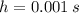
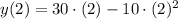
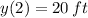
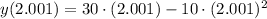
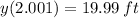
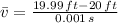
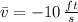
b) The instantaneous velocity when
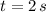 can be obtained by using the following limit:
can be obtained by using the following limit:
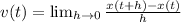
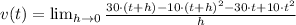
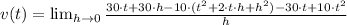
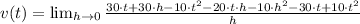
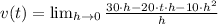

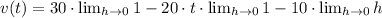
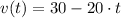
And we finally evaluate the instantaneous velocity at
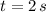 :
:
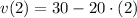

The instantaneous velocity of the ball when
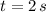 is
is
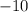 feet per second.
feet per second.