Question

On a coordinate plane, 2 lines are shown. Line P Q has points (negative 5, 3) and (5, 1). Line R S has points (negative 4, negative 2) and (0, negative 4).

Which statement best explains the relationship between lines PQ and RS?
They are parallel because their slopes are equal.
They are parallel because their slopes are negative reciprocals.
They are not parallel because their slopes are not equal.
They are not parallel because their slopes are negative reciprocals.

Answer 1

the correct answer is c

Explanation:

Edu2020

Answer 2

Given:

Line P Q has points (-5, 3) and (5, 1).

Line R S has points (-4, -2) and (0, -4).

To find:

The relationship between lines PQ and RS.

Solution:

If a line passing through two points, then the slope of line is

`m=(y_2-y_1)/(x_2-x_1)`

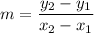
Line P Q has points (-5, 3) and (5, 1). So, slope of line PQ is

`m_1=(1-3)/(5-(-5))`

`m_1=(-2)/(5+5)`

`m_1=(-2)/(10)`

`m_1=(-1)/(5)`

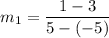
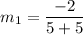
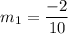
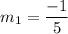
Line R S has points (-4, -2) and (0, -4). So, slope of line RS is

`m_2=(-4-(-2))/(0-(-4))`

`m_2=(-4+2)/(0+4)`

`m_2=(-2)/(4)`

`m_2=(-1)/(2)`

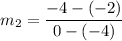
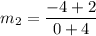
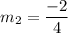
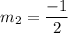
Slopes of two parallel lines are equal.

`m_1\\eq m_2`

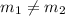
They are not parallel because their slopes are not equal.

Therefore, the correct option is C.