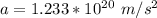Answer:
The value is
Step-by-step explanation:
From the question we are told that
The magnitude of the first charge is
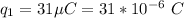
The position is y = 8 cm = 0.08 m
The magnitude of the second charge is
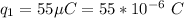
The position is x = 3 cm = 0.03 m
Generally the force exerted on the electron by the first charge is mathematically represented as

Here k is the coulombs constants with value
=>
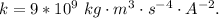
and e is the charge on a electron with value

So
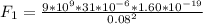

Generally the force exerted on the electron by the first charge is mathematically represented as
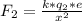
=>
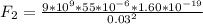
=>
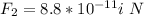
Generally the net force exerted is mathematically represented as
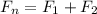
So
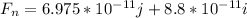
The resultant of this net force is mathematically represented as

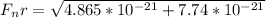
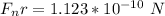
Generally this force can be represented as
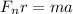
Here m is the mass of the electron with value

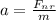
=>
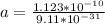
=>