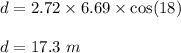Question

A worker on the roof of a house drops his 0.58 kg hammer, which slides down the roof at constant speed of 6.69 m/s. The roof makes an angle of 18 ◦ with the horizontal, and its lowest point is 18.2 m from the ground. what is the the horizontal distance traveled by the hammer between the time is leaves the roof of the house and the time it hits the ground?

Answer 1

17.3 m

Step-by-step explanation:

Given that,

Mass of a hammer is 0.58 kg

Velocity with which the hammer slides is 6.69 m/s at constant speed.

The roof makes an angle of 18 ◦ with the horizontal, and its lowest point is 18.2 m from the ground. We need to find the horizontal distance traveled by the hammer between the time is leaves the roof of the house and the time it hits the ground. Firstly, we will find the time taken by the hammer when it reaches ground in vertical direction.

`y=y_0+v_ot +(1)/(2)gt^2`

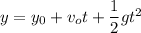
Putting all the values,

`0=18.2+6.69t-(1)/(2)* 9.8t^2\\\\-4.9t^2+6.69t+18.2=0\\\\t=\frac{-6.69+\sqrt{6.69^(2)-4\cdot-4.9\cdot18.2}}{2\cdot-4.9}, \frac{-6.69-\sqrt{6.69^(2)-4\cdot-4.9\cdot18.2}}{2\cdot-4.9}\\\\t=-1.36\ s\ \text{and}\ t=2.72\ s`

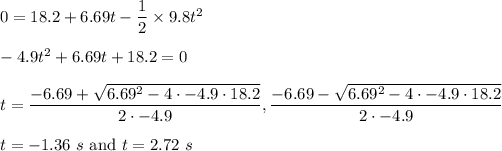
Neglecting negative value,

To find horizontal distance, multiply 2.72 s with the horizontal component of velocity.

`d=2.72* 6.69* \cos(18)\\\\d=17.3\ m`