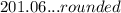Answer:
See Explanation!
Explanation:
Brief History:
While a circle, symbolically, represents many different things to many different groups of people including concepts such as eternity, timelessness, and totality, a circle by definition is a simple closed shape. It is a set of all points in a plane that are equidistant from a given point, called the center. It can also be defined as a curve traced by a point where the distance from a given point remains constant as the point moves. The distance between any point of a circle and the center of a circle is called its radius, while the diameter of a circle is defined as the largest distance between any two points on a circle. Essentially, the diameter is twice the radius, as the largest distance between two points on a circle has to be a line segment through the center of a circle. The circumference of a circle can be defined as the distance around the circle, or the length of a circuit along the circle. All of these values are related through the mathematical constant π, or pi, which is the ratio of a circle's circumference to its diameter, and is approximately 3.14159. π is an irrational number meaning that it cannot be expressed exactly as a fraction (though it is often approximated as 22/7) and its decimal representation never ends or has a permanent repeating pattern. It is also a transcendental number, meaning that it is not the root of any non-zero, polynomial that has rational coefficients. Interestingly, the proof by Ferdinand von Lindemann in 1880 that π is transcendental finally put an end to the millennia-old quest that began with ancient geometers of "squaring the circle." This involved attempting to construct a square with the same area as a given circle within a finite number of steps, only using a compass and straightedge. While it is now known that this is impossible, and imagining the ardent efforts of flustered ancient geometers attempting the impossible by candlelight might evoke a ludicrous image, it is important to remember that it is thanks to people like these that so many mathematical concepts are well defined today.
Solution: (Circle 1)
⇒ Given :
- Radius is 5
- Diameter is 10 (Can be known by adding the radius together.)
Using the formulas
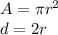
Solving for
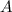
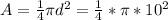 ≈
≈
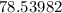
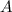 ≈
≈
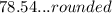
Solution: (Circle 2)
⇒ Given :
- Diameter is 16
- Radius is 8
Using the formulas
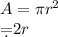
Solving for
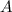
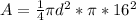 ≈
≈
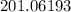
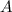 ≈
≈