Question

How would I solve y=9(x+3)(x-1) I need to find the vertex and the X intercepts​

Answer 1

See below ~

Explanation:

Finding the x-intercepts :

• The x-intercept's y-value is always 0
• 0 = 9(x + 3)(x - 1)
• x + 3 = 0 ⇒ x = -3
• x - 1 = 0 ⇒ x = 1
• So, hence the x-intercepts are : (-3, 0) and (1, 0)

Finding the vertex :

• Expand the polynomial from factorized form
• y = 9(x + 3)(x - 1)
• y = 9(x² + 3x - x - 3)
• y = 9(x² + 2x - 3)
• y = 9x² + 18x - 27
• Vertex = (h, k)
• h = -b/2a = -18/2(9) = -1
• k = 9(-1 + 3)(-1 - 1)
• k = 9(2)(-2)
• k = 9(-4) = -36
• Vertex = (-1, -36)

Answer 2

x-intercepts: x = 1 and x = -3

vertex: (-1, -36)

Explanation:

x-intercepts

x-intercepts are when y = 0

⇒ 9(x + 3)(x - 1) = 0

Divide both sides by 9:

⇒ (x + 3)(x - 1) = 0

Therefore:

⇒ (x + 3) = 0 ⇒ x = -3

⇒ (x - 1) = 0 ⇒ x = 1

Therefore the x-intercepts are x = 1 and x = -3

Vertex

Vertex form:
`y=a(x-h)^2+k` where (h, k) is the vertex

Completing the square

`\begin{aligned}y & =ax^2+bx+c\\& =a\left(x^2+(b)/(a)x\right)+c\\\\& =a\left(x^2+(b)/(a)x+\left((b)/(2a)\right)^2\right)+c-a\left((b)/(2a)\right)^2\\\\& =a\left(x-\left(-(b)/(2a)\right)\right)^2+c-(b^2)/(4a)\end{aligned}`

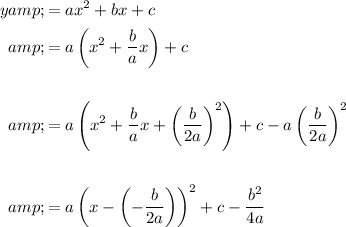
Therefore:

`y=9(x+3)(x-1)`

`\implies y=9x^2+18x-27`

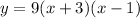
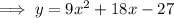
Completing the square to rewrite the equation in vertex form:

`\begin{aligned}y & =9x^2+18x-27\\& =9\left(x^2+(18)/(9)x\right)-27\\\\& =a\left(x^2+(18)/(9)x+\left((18)/(2(9))\right)^2\right)-27-9\left((18)/(2(9))\right)^2\\\\& =9\left(x-\left(-(18)/(2(9))\right)\right)^2-27-(18^2)/(4(9))\\\\& =9(x+1)^2-36\end{aligned}`

Therefore, the vertex is (-1, -36)