Answer:
(a) (7,39/2)
(b) Maximum, 39/2
(c) y ≤ 39/2
(d) Increase when x < 7 and decrease when x > 7
Explanation:
Given the parabola:
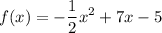
( A ) Find the vertex
In order to find the vertex, let’s use calculus for this one. Recall the power rules for differentiation:
Power Rules
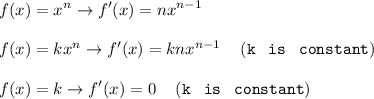
Derivative Definition
- Derivative f'(x) is a slope itself or rate of changes.
Derive the parabola:
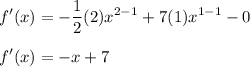
Since vertex has slope = 0 —> e.g f'(x) = 0:
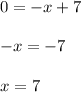
Substitute x = 7 in f(x):
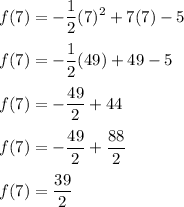
Therefore, the vertex is at (7,39/2)
( B ) Determine if max or min then find the value
Since the parabola opens downward then there only exists maximum value. The maximum value is the y-value of vertex at x-value of vertex. Henceforth:
- There is maximum value but no minimum value and the maximum value is 39/2 at x = 7.
( C ) Find range
For parabola, range is minimum value </≤ y </≤ maximum value. We know that parabola has maximum value of 39/2 but no minimum value so we can just ignore it then we’d have:
[Note: < and > are for open-dot meaning the value will not be included —> e.g x > 4 means 4 isn’t included in.]
( D ) Find the interval when function is increasing and when it’s decreasing
For parabola, the function will increase only if f'(x) or slope > 0 and will decrease only f'(x) < 0.
We know, from part A that the derivative is:
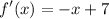
Therefore, when f'(x) > 0 —> e.g -x + 7 > 0:

When f'(x) < 0 —> e.g -x + 7 < 0:
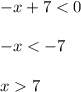
Therefore, the function will increase when x < 7 and will decrease when x > 7.