Question

Solve:||x-3|-2|≤1
Please show work!
Thanks

Answer 1

Explanation:

Hello,

We know that

`|x|=\begin{cases}x & \text{if } x\geq 0 \\ -x & \text{if } x<0 \end{cases}`

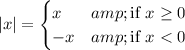
So we need to take into account two cases

Case 1 -
`x-3\geq 0<=> x\geq 3`

Then, |x-3|=x-3

||x-3|-2|=|x-3-2|=|x-5|

Either x-5 is positive and then |x-5|=x-5 and

`|x-5|\leq 1<=>x-5\leq 1<=>x\leq 6`

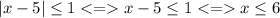
Or x-5 is negative and then, |x-5|=-x+5

`|x-5|\leq 1<=>-x+5\leq 1<=>4\leq x`

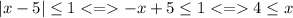
So the solution is [4;6]

Case 2 -
`x-3< 0<=> x< 3`

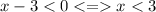
Then, |x-3|=-x+3

||x-3|-2|=|-x+3-2|=|-x+1|

Either -x+1 is positive and then |-x+1|=-x+1 and

`|-x+1|\leq 1<=>-x+1\leq 1<=>0\leq x`

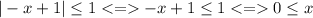
Or -x+1 is negative and then, |-x+1|=x-1

`|-x+1|\leq 1<=>x-1\leq 1<=>x\leq 2`

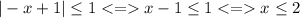
So the solution is [0;2]

Conclusion

The solution is [0;2]∪[4;6]

Thanks