Question

Find the distance between the two points. (round to the nearest hundredths)

distance:

Answer 1

`d=√(26)\approx5.10`

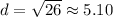
Explanation:

To find the distance between any two points, we can use the distance formula:

`d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2`

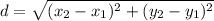
We can see that Point R is at (3,6), and Point E is at (8,5).

Let's let (3,6) be (x₁, y₁) and let's let (8,5) be (x₂, y₂). So, substituting them into our formula, we'll get:

`d=\sqrt{(8-3)^2+(5-6)^2`

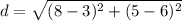
Subtract:

`d=\sqrt{(5)^2+(-1)^2`

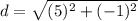
Square:

`d=√(25+1)`

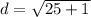
Add:

`d=√(26)`

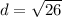
Approximate. Use a calculator:

`d=√(26)\approx5.10`

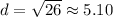
So, the distance between RE is approximately 5.1 units.

And we're done!

Answer 2

d = 5.10

Explanation:

The distance between two points is given by

d = sqrt( ( y2-y1)^2 + ( x2-x1)^2 ) where ( x1,y1) and ( x2,y2) are the two points

d = sqrt( ( 5-6)^2 + (8-3)^2 )

d = sqrt( ( -1)^2 + (5)^2 )

d = sqrt( 1+25)

d = sqrt(26)

d = 5.099019514

Rounding to the nearest hundredth

d = 5.10