Question

`\sqrt{2k ^(2) + 17 } - x = 0`

If k>0 and x=7 in the equation, what is the value of k?​

Answer 1

`k=4`

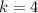
Explanation:

So we have the equation:

`√(2k^2+17)-x=0`

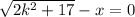
Where:

`k>0\text{ and } x=7`

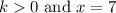
And we want to find k.

Firstly, let's substitute 7 for x. So:

`√(2k^2+17)-7=0`

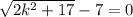
Now, we can solve for k. Add 7 to both sides:

`√(2k^2+17)=7`

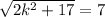
Square both sides:

`2k^2+17=49`

Subtract 17 from both sides:

`2k^2=32`

Divide both sides by 2:

`k^2=16`

Take the square root of both sides:

`k=\pm√(16)`

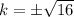
Evaluate:

`k=\pm 4`

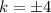
Remember that we are told k>0. In other words, k must be positive. So, we can ignore the negative answer, giving us:

`k=4`

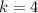
So, the value of k is 4.

And we're done!