Answer:
Option (1)
Explanation:
Perpendicular bisector of the segment will pass through the midpoint of the segment joining two points (5, 7) and (-3, 3).
Midpoint of the segment will be,
(x, y) =
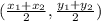
=
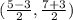
= (1, 5)
Slope of the line joining the given points
 =
=
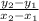
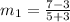
=

Let the slope of the line perpendicular to the segment joining the given points is
 .
.
By the property of perpendicular lines,
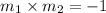
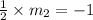
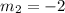
Since, equation of a line passing through (x', y') and slope 'm' is,
y - y' = m(x - x')
Therefore, equation of the line passing through (1, 5) and slope (-2) will be,
y - 5 = (-2)(x - 1)
y = -2x + 2 + 5
y = -2x + 7
2x + y = 7
Therefore, Option (1) will be the answer.