Since Porsche’s mom told her to choose 3 crayons out if a box of 64, the probability that she will choose the red, yellow and blue crayons is 1/6.
In Mathematics, a combination should be used when selecting more than one item without replacement and order is not important. Based on the information provided, we can logically deduce that the order in which Porsche chooses the crayons does not matter, so we would apply a combination.
Since there are 64 items in the box and she will only choose 3 crayons, the total number of ways that she can choose any 3 crayons is given by;
Total number of ways (3 crayons) = 64 × 63 × 62
Total number of ways (3 crayons) = 249984 ways.
In this context, the completed formula for this combination can be written as follows;
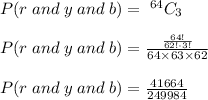
Next, we would reduce the fraction to its simplest form by dividing all through with 41664;
P(r and y and b) = 1/6.
Complete Question:
Porsche’s mom told her to choose 3 crayons out if a box of 64. What is the probability she will choose red, yellow and blue?