Question

Adam invests $6,139 in a retirement account with a fixed annual interest rate compounded continuously. After 17 years, the balance reaches $8,624.97. What is the interest rate of the account

Answer 1

An account with a starting balance of P accruing interest with rate r for time t, componunded continuously, ends up with a balance A according to

`A=Pe^(rt)`

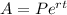
Plug in everything you know and solve for r :

`8624.97=6139e^(17r)`

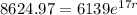
Divide both sides by 6139:

`(8624.97)/(6139)=e^(17r)`

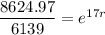
Take the natural logarithm of both sides:

`\ln\left((8624.97)/(6139)\right)=\ln e^(17r)`

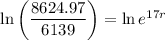
Recall that
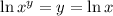`\ln x^y=y=\ln x`, so that

`\ln\left((8624.97)/(6139)\right)=17r\ln e`

and ln(e) = 1, so

`\ln\left((8624.97)/(6139)\right)=17r`

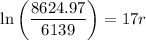
Finally, divide both sides by 17:

`r=\frac1{17}\ln\left((8624.97)/(6139)\right)=\boxed{0.02}`

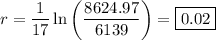
So the account has an interest rate of 2%.