Question

PLEASE HELP! 40 points!! I've been stuck on this for 30 minutes constantly coming up with all different answers, please help me.

What is the area of rhombus ABCD?



Enter your answer in the box. Do not round at any steps.

______units²

Answer 1

36 units^2

Explanation:

The area of a triangle is 1/2*base*height. Knowing this is just 2 triangles means you solve for 1 triangle, then multiply that by 2

Answer 2

`A=36\text{ units}^2`

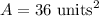
Explanation:

The area of a rhombus is given by the formula:

`A=(d_1\cdot d_2)/(2)`

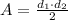
Namely, it is half of one diagonal multiplied by the other diagonal.

So, to find the area, we just need to find the length of AC and BD, multiply them together, and then divide by 2.

To find their lengths, we can use the distance formula. The distance formula is:

`d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2`

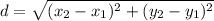
So, let's find the lengths of each diagonal:

AC:

Point A is (-1,0) and Point C is (-1,-6). Let (-1,0) be (x₁, y₁) and let (-1,-6) be (x₂, y₂). Substitute this into our formula:

`d=\sqrt{(-1-(-1))^2+(-6-0)^2`

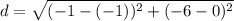
Simplify:

`d=\sqrt{(-1+1)^2+(-6-0)^2`

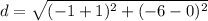
Add or subtract:

`d=\sqrt{(0)^2+(-6)^2`

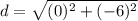
Square:

`d=√(36)`

Take the square root:

`d=6`

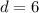
So, the length of diagonal AC is 6.

BD:

Point B is at (5,-3) and Point D is at (-7,-3). Let (5,-3) be (x₁, y₁) and let (-7,-3) be (x₂, y₂). Substitute this into our formula:

`d=\sqrt{(-7-5)^2+(-3-(-3))^2`

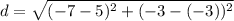
Simplify:

`d=\sqrt{(-7-5)^2+(-3+3)^2`

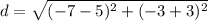
Add or subtract:

`d=\sqrt{(-12)^2+(0)^2`

Square:

`d=√(144)`

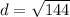
Take the square root:

`d=12`

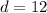
So, our second diagonal is 12 units long.

Now, to find the area, substitute 6 and 12 into our formula. So:

`A=(d_1\cdot d_2)/(2)`

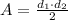
Substitute 6 for d₁ and 12 for d₂. So:

`A=((6)(12))/(2)`

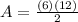
Multiply:

`A=(72)/(2)`

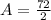
Divide:

`A=36\text{ units}^2`

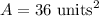
So, the area of the rhombus is 36 squared units.

And we're done!

Notes:

Of course, instead of using the distance formula, you can also just count :)