Question

Two balls are thrown against a wall. Ball 1 has a much higher speed than ball 2.

Explain how the energy of the two balls is different.

Answer 1

Let both the balls have the same mass equals to m.

Let
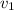`v_1` and
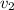`v_2` be the speed of the ball1 and the ball2 respectively, such that

`v_1>v_2\;\cdots(i)`

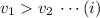
Assuming that both the balls are at the same level with respect to the ground, so let h be the height from the ground.

The total energy of ball1= Kinetic energy of ball1 + Potential energy of ball1. The Kinetic energy of any object moving with speed,
`v`, is
`\frac 12 m v^2`

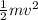
and the potential energy is due to the change in height is
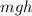`mgh` [where
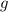`g` is the acceleration due to gravity]

So, the total energy of ball1,

`=\frac 12 m v_1^2 + mgh\;\cdots(ii)`

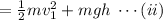
and the total energy of ball1,

`=\frac 12 m v_2^2 + mgh\;\cdots(iii)`.

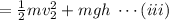Here, the potential energy for both the balls are the same, but the kinetic energy of the ball1 is higher the ball2 as the ball1 have the higher speed, refer equation (i)

So,
`\frac 12 m v_1^2 >\frac 12 m v_2^2`

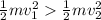
Now, from equations (ii) and (iii)

The total energy of ball1 hi higher than the total energy of ball2.