Assuming that you want the product of the two factors given in each problem:
⇒ we solve this problem by timing each unit of a factor to every unit
of the other factor
⇒then add each one of them who shares a common like-term
⇒to get the answer
Let's solve:
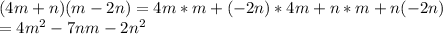
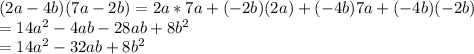
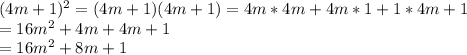
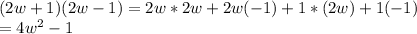
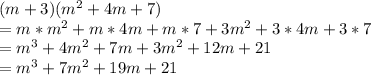
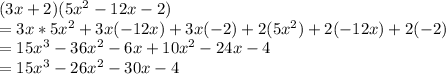
Hope that helps!