Question

2. A sphere has a great circle whose circumference is 95 centimeters. Which of the following is closest to the

volume of the sphere, in cubic centimeters?
1) 4,600
(3) 12,700
2) 7,500
(4) 14,500

Answer 1

Approximately
`14,\!500\; {\rm cm^(3)}`.

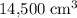Explanation:

The radius of a sphere is the same as the radius of the great circle of that sphere.

Thus, in this question, it would be possible to find the radius of the sphere by finding the radius of the great circle.

The circumference of a circle of radius
`r` is
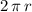`2\, \pi \, r`. In this question, it is given that the circumference of this great circle is
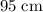`95\; {\rm cm}`. Thus, the radius of this great circle would be:

`\begin{aligned}r &= \frac{95\; {\rm cm}}{2\, \pi} \approx 15.1197\; {\rm cm}\end{aligned}`.

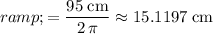Thus, radius of the sphere in this question would also be approximately
`15.1197\; {\rm cm}`.

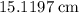The volume of a sphere of radius
`r` is
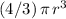`(4/3)\, \pi\, r^(3)`. Thus, the volume of this sphere of radius
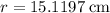`r = 15.1197\; {\rm cm}` would be approximately:

`\begin{aligned}(4)/(3) \, \pi* (15.1197\; {\rm cm})^(3) \approx 14,\!500 \; {\rm cm^(3)}\end{aligned}`